Author Archives: sowrdes

The Rijndael block cipher first creates a key from the key schedule, runs an initial round, and then starts its main rounds. There are four steps of the main rounds: 1) SubBytes, 2) ShiftRows, 3) MixColumns, and 4) AddRoundKey. One defining aspect of the Rijndael cipher is that it takes place inside a Galois field defined as GF(2⁸).  This plays a key part in the SubBytes and the MixColumns step. Another defining aspect is that the first step is to change the 128-bit plain text into a binary, and then to put it in a 4×4 matrix. This 4×4 matrix is called the state and it is what all future steps operate on. Each byte in the 4×4 matrix is composed of 8 bits and represents one character. The first step, SubBytes is the substitution part of the cipher, and the second and third steps, ShiftRows and MixColumns, are the permutation parts of the cipher.

128-bit example text: The cat flew!!!!

Convert to binary: 01010100 01101000 01100101 00100000 01100011 01100001 01110100 00100000 01100110 01101100 01100101 01110111 00100001 00100001 00100001 00100001

Put in a 4×4 state:

01010100	01100011	01100110	00100001
01101000	01100001	01101100	00100001
01100101	01110100	01100101	00100001
00100000	00100000	01110111	00100001

A Galois field is a finite field where addition, subtraction, multiplication, or division can be performed on the elements. What makes it finite is that whenever a result greater than 2⁸, (or 256) is achieved, the modulus operation is applied, and the result instead wraps back around to the beginning of the field. This keeps all the results inside the field and is crucial to the Rijndael S-box that is used in the first step, SubBytes.

AES S-box

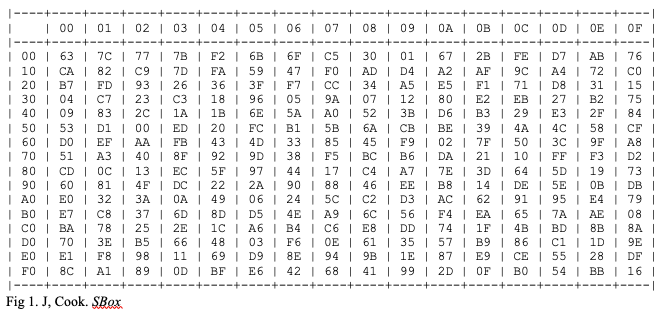
The math required to map a value to its corresponding S-box value is quite complicated and is one reason the Rijndael cipher is so strong. The polynomial used in Rijndael’s Galois field is x⁸+x⁴+x³+x+1, and the S-box value is mapped based on first the multiplicative inverse over the Galois field, and then by using an affine transformation. The SubBytes step maps each corresponding byte to a value in the S-box. On the S-box, the columns are determined by the least and most significant nibbles of the byte, converted into hexadecimal form. The result of this step is that the original sixteen bytes in the 128bit block have been mathematically manipulated to another of 4×4 table of practically untraceable bytes.

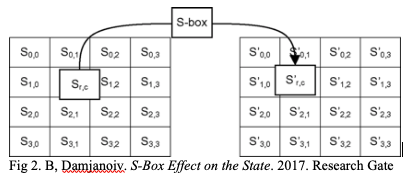
Fig 2. B, Damjanoiv. S-Box Effect on the State. 2017. Research Gate

The next step, ShiftRows, is the simplest step in the round. The first row is not shifted, but the second row is shifted left by one, the third row is shifted left by 2, and the fourth row is shifted left by three. This adds the first layer of permutation.

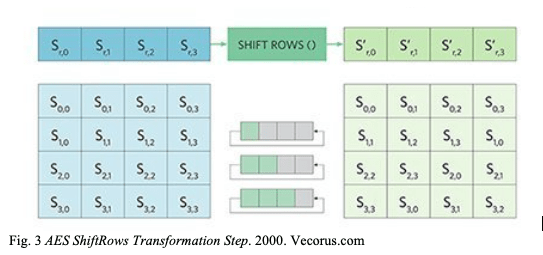
Fig. 3 AES ShiftRows Transformation Step. 2000. Vecorus.com

The third step, MixColumns, adds the second layer of permutation.  Each column is multiplied by a fixed matrix (inside the Galois field) to produce a new byte. The specific math of the matrix multiplication is that each column is treated as a polynomial in the form  and then multiplied with the fixed polynomial  mod .  

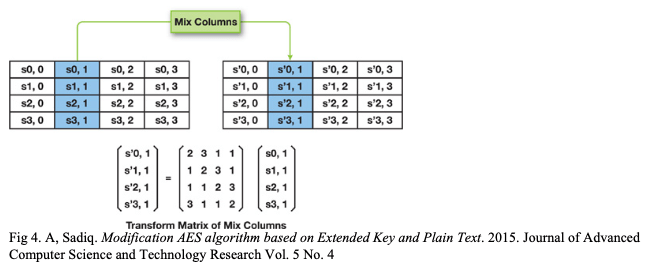
Fig 4. A, Sadiq. Modification AES algorithm based on Extended Key and Plain Text. 2015. Journal of Advanced Computer Science and Technology Research Vol. 5 No. 4

The last step of the round AddRoundKey is to XOR the resultant 4×4 state block bitwise with the round-specific subkey determined by the key schedule, which produces the final encrypted state of the 128-bit block.

These steps are repeated either 10, 12, or 14 times depending on the length of the key. In the last round, the MixColumns step is omitted. Although the Rijndael cipher uses very complicated math to produce the cipher text, each step has a mathematical inverse that makes decrypting (with the proper key) a swift feat.

Daemen, J., & Rijmen, V. (1999, September 3). AES Proposal: Rijndael. Retrieved December 5, 2019, from https://csrc.nist.gov/csrc/media/projects/cryptographic-standards-and-guidelines/documents/aes-development/rijndael-ammended.pdf.

Easttom, C. (2016). Modern Cryptography. McGrawHill Education.

Pound, M. (2019, November 22). AES Explained – Computerphile. Retrieved December 5, 2019, from https://www.youtube.com/watch?v=O4xNJsjtN6E.

(first draft!)

Quantum cryptography, although still in its infancy, offers to change the landscape of cryptography in the next couple of decades. The recent ramp up in breakthroughs with quantum technology is comparable to the rate of computer development after the first transistor was invented in 1947: seeing as it took roughly 30 years for computers to become an integral part of business, and another 30 years for computers to become embedded into everyday life, we might see a similar timeline with quantum computing and its applications in cryptography.

In the late 1960’s, a physics research student at Columbia University, Stephen J. Wiesner conceptualized the first modern ideas in quantum information theory: conjugate coding, which is the idea that information can be transmitted in such a way using polarized photons that reading a part of the message destroys the rest of the message. After 40 years of research, in 1998 the first working quantum computer is built, and we see the first instance of a quantum algorithm in use. Fast forward to 2018, and we have the global commercialization of Quantum Key Distribution via the company Quantum Xchange. Quantum Key Distribution (QKD) isn’t necessarily quantum cryptology but is an application of quantum processes that relate to the current field of cryptology. QKD provides a way of securely transmitting a key so that two parties can use a shared secret key with assurance that the secret has not been sniffed. There are two ways of doing this: sending photons with encoded information through fiber optic cables (which is what Quantum Xchange does), and to quantum entangle two particles, then encode qubits of information on one particle and let spooky action at a distance replicate the information on the other entangled particle. (So far, China has been a pioneer in using satellites to transmit quantumly entangled information over distances of 1200kms, which would potentially lay the groundwork for a global quantum communication network.) A “qubit” is the most basic unit of quantum information and can relay an electrons spin (up or down), or polarization (horizontal or vertical). Due to the strangeness of quantum mechanics if a qubit is measured the electron will change state, which is the underlying principal of conjugate coding and QKD key security. A key can be communicated via a chain of qubits, and if an unauthorized third party tries to sniff the information, the electrons will change state, become untangled, and the key will be unusable. Seeing as how currently some important secret keys in the financial and government sectors are transmitted physically via carrier, QDK could fill an important part in corporate and government security.

In the news, quantum cryptography has been heralded as a destroyer of all current cryptographical systems. While that does have some truth, most worries are significantly blown out of proportion. The most reasonable threat to current cryptography would be in the form of the Grover and Shor algorithms: Gover’s algorithm “gauges the probabilities of various potential states of the system” (CITATION: CODEBURST.IO), and Shor’s algorithm reduces the time a system takes to search for the factors of large prime numbers. In an article published by the International Journal of Advanced Computer Science and Applications, some realistic threats are outlined: public key algorithms based on factorization and discrete logs (such as RSA, ElGamal, and elliptic curves), especially those with tiny key spaces (such as elliptic curve) are especially vulnerable to cracking via Shor’s algorithm. However, symmetric key algorithms with large key sizes such as AES are resistant to current quantum algorithms. Currently only the Grover algorithm offers a threat, but only on keys with small key sizes. Similarly, most hashes with large outputs are resistant.

Quantum computing quite a long way to go before the cryptographic community should start sounding storm warnings. Of course, it’s never too early to start preparing, but there are some base developments that have to happen before current cryptology is legitimately threatened. First, these potential key cracks using quantum algorithms require a quantum computer with many more qubits than is currently possible. An article published in 2008 from the University of Waterloo says a 1024-bit RSA key would require 2000 qubits to break, and a 160-bit ECC key would require 1000 qubits. As of November 2019, the largest known working quantum computer is a 53-qubit machine owned by IBM. (D-Wave Systems recently announced a generation of quantum chips that have 5,000-qubits, but so far that is only theoretical). The amount of qubits a quantum computer has is limited by a few things, one being the fact that electrons are whimsical and need to be kept close to absolute zero (-459 Fahrenheit) in order to maintain their quantum states. For example, one of the IBM 20-qubit computers is housed in a 729sq ft. air-tight glass cube that is kept near absolute zero to keep the electrons in line. Needless to say, setups like these require immense resources. Another limitation is that due to the nature of electrons and quantum probability, having all the qubits in a machine provide reliable information is in itself a feat, and is still a large problem that requires solutions before quantum computers will reach the size necessary to crack current cryptography. Another issue is that creating quantum algorithms may exist in theory, but actually applying them to a quantum machine is almost as difficult as creating the algorithm. Just like current day computers, quantum computers require a language, programming syntax, instructions sets (equivalent to machine languages) and have to be tailored to individual systems. Currently there are a handful of quantum programming languages out there who’s applications are being developed, such as Q#, QCL, and LanQ.

Quantum cryptography will absolutely change how the world uses cryptography, but those changes are still a while off, and if realistic measures are taken now, such as researching mathematical limits of quantum key-cracking (such as lattice or code-based cryptology), information that is currently secure can remain secure in the future.